Answer:
60.46%
Explanation:
Question: On this dartboard, the circle with 1-m radius is inscribed in an equilateral triangle. Find the probability that a dart that hits the board lands in the circular region. Justify your answer.
Let's start by finding the length of one of the sides of the equilateral triangle. We can do this by creating a 30-60-90 triangle from the radius of the inscribed circle.
I attached an image of what this should look like.
Solving for the length of half of the base of the equilateral triangle gives us 1√3. To get the length of the entire base of the triangle, we will double this value:
The area of an equilateral triangle is
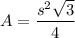 .
.
We can substitute the known value of s (side length) into the formula and solve for A.
The area of the equilateral triangle is 3√3.
Now, let's solve for the area of the inscribed circle. The formula for the area of a circle is
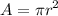 .
.
We know the radius of the circle is 1, so let's substitute 1 for r:
The area of the inscribed circle is π.
To find the probability of the dart hitting a specific area on the dartboard, we will divide the desired area by the total area of the dartboard.
The probability that a dart that hits the board lands in the circular region is about 60.46%.