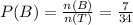Question

12,15,7 in a simplified fraction

Answer 1

The probability of landing on red is;

`(6)/(17)`

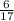
The probability of landing on yellow is;

`(15)/(34)`

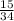
The probability of landing on blue is;

`(7)/(34)`

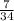
Step-by-step explanation:

Given the colors and frequencies as;

`\begin{gathered} \text{ Red = 12} \\ \text{ Yellow = 15} \\ \text{Blue = 7} \\ \text{Total = 34} \end{gathered}`

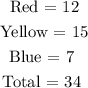
The probability of landing on red is;

`P(R)=(n(R))/(n(T))=(12)/(34)=(6)/(17)`

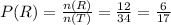
The probability of landing on yellow is;

`P(Y)=(n(Y))/(n(T))=(15)/(34)`

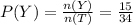
The probability of landing on blue is;

`P(B)=(n(B))/(n(T))=(7)/(34)`