Question

Which of the following explicit equations represents the sequences -5,10,20,40 EXPLAIN PLSS

Answer 1

we have the sequence

5,10,20,40,...

so

a1=5 ----> first term

a2=10

a3=20

a4=40

a2/a1=10/5=2

a3/a2=20/10=2

a4/a3=40/20=2

we have a geometric sequence with a common ratio r=2

the equation is of the form

`r(n)=a_1\cdot r^((n-1))`

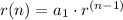
substitute given values

`\begin{gathered} r(n)=5\cdot2^((n-1)) \\ r(n)=5\cdot2^n\cdot2^(-1) \\ r(n)=5\cdot2^n\cdot(1)/(2) \\ r(n)=2.5\cdot2^n^{} \end{gathered}`

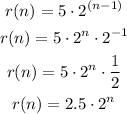
the answer is the first option