Given:
The probability that a baby that is born is a boy is
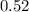
And the probability that a baby that is born is a girl is
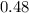
Required:
We have to find the probability that the family has 0, 1, or 2 girls.
Step-by-step explanation:
Let B denote the event that a baby that is born is a boy and G denote the event that a baby that is born is a girl.
The given that
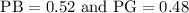
We solve this problem by using the formula of the binomial distribution.
The probabilty of