Question

A bag contains 2 gold marbles, 8 silver marbles, and 29 black marbles. Someone offers to play this game: You randomly select one marble from the bag. If it is gold, you win $4. If it is silver, you win $2. If it is black, you lose $1.What is your expected value if you play this game?

Answer 1

The bag contains:

2 gold marbles

8 silver marbles

29 black marbles

Prizes:

$4 if it's gold

$2 if it's silver

$1 if it's black

We can calculate the expected value using the following formula:

`E(x)=\sum ^3_(i\mathop=1)x_i\cdot P(x_i)`

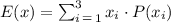
Where xi is the money you can get for each marble and P is its probability

Gold marble:

x = $4

P(x) =

`P=(2)/(2+8+29)=(2)/(39)`

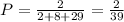
then, x*p(x) is

`4\cdot(2)/(39)=(8)/(39)`

Silver marble:

x = $2

P(x) =

`P=(8)/(2+8+29)=(8)/(39)`

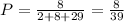
then, x*p(x) is

`2\cdot(8)/(39)=(16)/(39)`

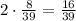
Black marble:

x = $-1

P(x) =

`P=(29)/(2+8+29)=(29)/(39)`

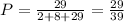
then x*p(x) is

`-1\cdot(29)/(39)=-(29)/(39)`

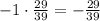
Finally, we need to add all those x*p(x) values we got before to find the expected value, this is:

`E(x)=\sum ^3_{i\mathop{=}1}x_i\cdot P(x_i)=(8)/(39)+(16)/(39)-(29)/(39)=-(5)/(39)\cong-0.1282`

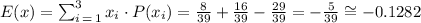
Answer: your expected value if you play this game is -0.1282