We have the following functions
![g\mleft(x\mright)=\frac{1}{\sqrt[]{x}},f(x)=x^2-4](https://img.qammunity.org/2023/formulas/mathematics/high-school/byuycolqlif180g8s0g2zbhyea5af2ntsh.png)
Let's determine the domain of the following:
1. domain of g(x)/f(x):
![(g(x))/(f(x))=\frac{\frac{1}{\sqrt[]{x}}}{x^2-4}](https://img.qammunity.org/2023/formulas/mathematics/high-school/aobr02r42navjj5uldi7ctxldp4za0ipno.png)
Let's simplify the above
![\begin{gathered} =\frac{1}{\sqrt[]{x}\cdot(x^2-4)} \\ =\frac{1}{\sqrt[]{x}}\cdot(1)/(x^2-4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ad49jn7dpn0jmnfo2l0ow01au4nadach1k.png)
The above it's like having to functions, hence two domains:
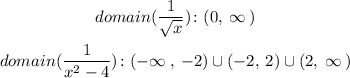
Therefore, the domain of g/f (x) is:
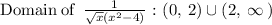
2. domain of g(f(x)):
![g(f(x))=g(x^2-4)=\frac{1}{\sqrt[]{x^2-4}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9egp6tpue17kb1byjh8e12bht9uauwhr0i.png)
Since, x^2-4 > 0, therefore domain of g(f(x)) is the following:
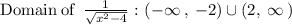
3. domain of f(g(x)):
![f(g(x))=f(\frac{1}{\sqrt[]{x}})=(\frac{1}{\sqrt[]{x}})^2-4](https://img.qammunity.org/2023/formulas/mathematics/high-school/x9qimjw839dz4vtfw3xkcu5smtcr3ksazz.png)
Since, x>0, Therefore, the domain of f(g(x)) is:
![domain(\frac{1}{\sqrt[]{x}}^2-4)\colon(0,\infty)](https://img.qammunity.org/2023/formulas/mathematics/high-school/ol5iwwwu0mjzpo7v8bphrmscj0went9m0o.png)