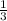Question

f(x) = x2 + bxg(x) = 3x2 - 9xThe functions f and g are defined above, where b is a constant. Iff(x) (x) = 3x4 – 8x3 – 3x2, what is the value of b?

Answer 1

Given the functions:

`\begin{gathered} f(x)=x^2+bx \\ \\ g(x)=3x^2-9x \\ \\ f(x)*g(x)=3x^4-8x^3-3x^2 \end{gathered}`

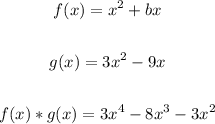
Let's find the value of b.

Let's multiply the individual functions.

Solving further, we have:

`\begin{gathered} f(x)*g(x)=(x^2+bx)(3x^2-9x) \\ \\ \text{ Expand using FOIL method:} \\ x^2(3x^2-9x)+bx(3x^2-9x) \end{gathered}`

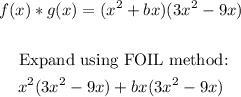
Apply distributive property:

`f(x)*g(x)=3x^4-9x^3+3bx^3-9bx^2`

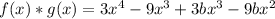
Now, to match this expression to the given expression let's check a value we can input for b.

Take b = 1/3.

Substitute 1/3 for b and simplify:

`\begin{gathered} f(x)*g(x)=3x^4-9x^3+3((1)/(3))x^3-9((1)/(3))x^2 \\ \\ =3x^4-9x^3+1x^3-3x^2 \\ \\ =3x^4-8x^3-3x^2 \end{gathered}`

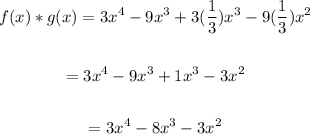
Therefore, the value of b is 1/3

ANSWER:

`(1)/(3)`