Question

Identify the domain, vertical asymptotes and horizontal asymptotes of the following rational function

Answer 1

Given the rational function

`f(x)=(3x-4)/(x^3-16x)`

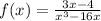
Set the denominator equals zero and find the roots.

`\begin{gathered} x^3-16x=0 \\ x(x-4)(x+4)=0 \\ x=0,4,-4 \end{gathered}`

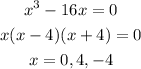
The denominator is equal to zero when x = 0, 4,-4.

The domain of the function is all real numbers except the three points x=0, x=4 and x=-4.

Now, find the vertical asymptotes.

Firs, factor the numerator and denominator.

`f(x)=(3x-4)/(x(x-4)(x+4))`

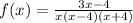
To find the vertical asymptotes, determine where this function will be undefined by setting the denominator equal to zero.

`\begin{gathered} x(x-4)(x+4)=0 \\ x=0,4,-4 \end{gathered}`

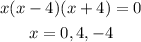
Neither x=0, x=4 nor x=-4 are zeros of the numerator, so the three values indicate three vertical asymptotes.

Now, find the horizontal asymptotes.

If the degree of numerator is less than degree of denominator, then the horizontal asymptote at y = 0.

Here, the degree of the numerator is 1 and the degree of the denominator is 3. So, the degree of the numerator is less than the degree of the denominator. Hence the horizontal asymptote at y = 0.