Given are the points of the vertices of the triangle.
A ( -4 , -7 )
B ( 8, 2 )
C ( -6, 8 )
Required:
a) slope of line AB
b) equation of the line that passes through C and is perpedicular to AB
c) coordinates of D which is the intersection of AB and the line that passes through C
d) the kind of triangle CBD and CAD
Solution :
a) slope of line AB
A ( -4 , -7 )
B ( 8, 2 )
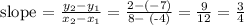
b) equation of the line that passes through C and is perpedicular to AB.
The slopes of two perpendicular lines are negative reciprocals of each other. Therefore, the slope of the line that passes through C ( -6, 8 ) is
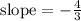
The point-slope form of a line is :

where m is the slope = -4/3
at point C ( -6, 8)
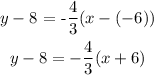
c) coordinates of D which is the intersection of AB and the line that passes through C
Equation of line AB : Let's take point A ( -4 , -7 ) and slope is 3/4 . Using the point intercept form:

Equation of the line that passes through C:
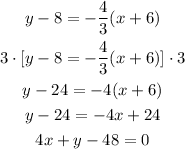
The point of intersection of line


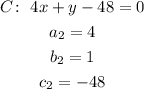
The point of intersection, D:
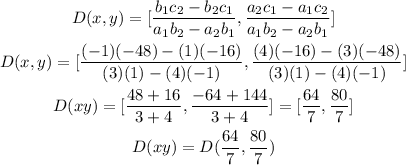
d) the kind of triangle CBD and CAD
Both triangles are right triangle , since sline CD is perpendicular to line AB