Question

In the process of elimination method which step did an error occur?

Answer 1

Given the system

`\begin{gathered} 2x+y=4 \\ 6x-2y=6 \end{gathered}`

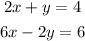
First step, the first equation is multiplied by -3

`\begin{gathered} -3(2x+y)=-3\cdot4 \\ -3\cdot2x-3\cdot y=-12 \\ -6x-3y=-12 \end{gathered}`

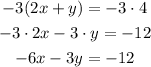
Step 2, add both equations, you have to add the like terms

`\begin{gathered} (-6x-3y)+(6x-2y)=-12+6 \\ -6x+6x-3y-2y=-12+6 \\ 0x-5y=-6 \\ -5y=-6 \end{gathered}`

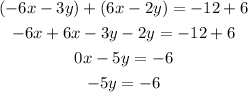
Step 3 divide both sides by -5 to determine the value of y

`\begin{gathered} -(5y)/(-5)=-(6)/(-5) \\ y=(6)/(5) \end{gathered}`

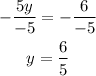
Step 4 determine the value of x, by replacinf y=6/5 in the first equation

`\begin{gathered} 2x+y=4 \\ 2x+(6)/(5)=4 \\ 2x=4-(6)/(5) \\ 2x=(14)/(5) \\ (2x)/(2)=((14)/(5))/(2) \\ x=(14)/(5)\cdot(1)/(2) \\ x=(7)/(5) \end{gathered}`

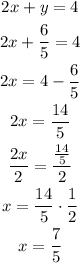
Solution (7/5, 6/5)

The error is in step 3, (-3y)+(-2y)=-5y NOT -y