Question

Hi, can you help me answer this question, please, thank you:)

Answer 1

Given:

32% are yellow

68% are green

number of samples = 49 eggs

The distribution is binomial because we can either have a green or yellow egg.

(a) The mean number of yellow eggs in samples of 49 eggs

The mean can be calculated using the formula:

The probability (p) of success is the percentage of yellow eggs which is:

`p\text{ = 0.32}`

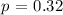
Substituting to get the mean:

Hence, the mean number of yellow eggs in the sample is 15.68

(b) The variance in the number of yellow eggs in the sample

The variance can be calculated using the formula:

`\text{variance = np(1-p)}`

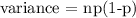
Substituting we have:

`\begin{gathered} \text{variance = 49 }*\text{ 0.32 }*\text{ (1-0.32)} \\ =\text{ 10.6624} \end{gathered}`

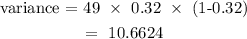
Hence, the variance in the number of yellow eggs in the sample is 10.6624

(c) The standard deviation in the number of yellow eggs in the sample

Standard deviation can be calculated from the variance using the relationship:

`\begin{gathered} \sigma\text{ = }\sqrt[]{variance} \\ =\text{ }\sqrt[]{10.6624} \\ \approx\text{ 3.2653 (4.d.p)} \end{gathered}`

Hence, the standard deviation in the number of yellow eggs in the sample is 3.2653