Question

The standard form for a parabola with vertex (h,k) and an axis of symmetry of x=h is:(x-h)^2=4p(y-k)The equation below is for a parabola. Write it in standard form. When answering the questions type coordinates with parentheses and separated by a comma like this (x,y). If a value is a non-integer then type is a decimal rounded to the nearest hundredth. (x+4)^2=24(y+1)The value for p is: AnswerThe value for h is: AnswerThe value for k is: AnswerThe focus is the point: AnswerThe directrix is the line y=Answer

Answer 1

The value for p is 6.

The value for h is -4.

The value for k is -1.

The focus is at (h, k+p) = (-4, 5).

The directrix is the line y = -7.

Step-by-step explanation:

Given the equation of parabola

`(x+4)^2=24(y+1)`

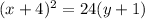
Write in standard form.

`(x-(-4))^2=4\cdot6(y-(-1))`

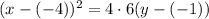
Comaparing with

`(x-h)^2=4p(y-k)`

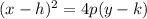
gives h = -4, p = 6 and k = -1.

The value for p is 6.

The value for h is -4.

The value for k is -1.

The focus is at (h, k+p) = (-4, -1+6) = (-4, 5).

The directrix is the line y = k-p.

Substituting the values gives y = -1 - 6 = -7.

So, the directrix is the line y = -7.