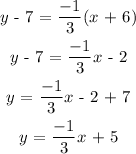Question

Example(-6,7)(-3,6)Find the slopeWrite in point slopeWrite in slope intercept form

Answer 1

Answer:
`\begin{gathered} \text{Slope = }(-1)/(3) \\ y\text{ - 7 = }(-1)/(3)(x\text{ + 6) (Point-slope form)} \\ y\text{ = }(-1)/(3)x\text{ + 5 (Slope-intercept form)} \end{gathered}`

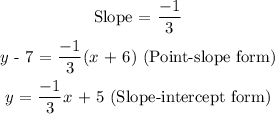
Explanations:

The slope of a line is calculated using the formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

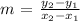
For the points (-6, 7) and (-3, 6)

`\begin{gathered} x_1=-6,y_1=7,x_2=-3,y_2=6 \\ m\text{ = }(6-7)/(-3-(-6)) \\ m\text{ = }(-1)/(3) \end{gathered}`

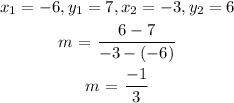
The slope = -1/3

The point-slope form of the equation of a line is:

`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 7 = }(-1)/(3)(x\text{ - (-6))} \\ y\text{ - 7 = }(-1)/(3)(x\text{ + 6)} \end{gathered}`

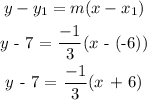
To find the slope-intercept form, reduce the equation above to the form:

y = mx + c

`\begin{gathered} y\text{ - 7 = }(-1)/(3)(x\text{ + 6)} \\ y\text{ - 7 = }(-1)/(3)x\text{ - 2} \\ y\text{ = }(-1)/(3)x\text{ - 2 + 7} \\ y\text{ = }(-1)/(3)x\text{ + 5} \end{gathered}`