Question

Given that cos A= 1/V37 and cos B = 1/V2, and that angles A and B are both inQuadrant I, find the exact value of cos(A + B), in simplest radical form.

Answer 1

Given:

CosA = 1/√37

Cos B = 1/√2

Using the identity below:

`\text{Cos(A}+B)=\cos A\cos B-\sin A\sin B`

We need to find sinA

Using the identity

cos²A + sin²A= 1

Substitute cosA = 1/√37 into the above and solve for sinA

(1/√37) ² + sin²A = 1

1/37 + sin²A = 1

Subtract 1/37 from both-side of the equation

sin²A = 1- 1/37

`\sin ^2A=(37-1)/(37)=(36)/(37)`

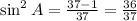
Take the square root of both-side

`\sin A=\pm\sqrt[]{(36)/(37)}=\pm\frac{6}{\sqrt[]{37}}`

But sinA is in the first quadrant, hence it is positive.

sinA = 6/√37

Next, is to find the value of sinB.

cos²B + sin²B= 1

Substitute for cosB and solve for sinB.

(1/√2)² + sin²B = 1

1/2 + sin²B = 1

Subtract 1/2 from both-side of the equation.

sin²B = 1 - 1/2

`\sin ^2B=(2-1)/(2)=(1)/(2)`

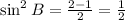
Take the square root of both-side of the equation.

`\sin B=\pm\frac{1}{\sqrt[]{2}}`

sine is positive in the first quadrant, hence sinB = 1/√2

We can now proceed to solve for cos(A+B)

`\text{Cos(A}+B)=(\frac{1}{\sqrt[]{37}})(\frac{1}{\sqrt[]{2}})-(\frac{6}{\sqrt[]{37}})(\frac{1}{\sqrt[]{2}})`

`=\frac{1}{\sqrt[]{74}}-\frac{6}{\sqrt[]{74}}`

`=-\frac{5}{\sqrt[]{74}}`