Question

solve if possible. if not, indicate what information is needed.The width of a rectangle is 6 inches less than its length. the area of the rectangle is 135 inches squared. find the length and width.

Answer 1

Let L be the length of the rectangle, measured in inches.

Since the width is 6 inches less than its length, then the width is equal to:

`L-6`

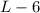
The area of the rectangle is equal to the product of its length and its width. Then, the area is given by the expression:

`(L)(L-6)`

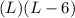
Which is equal to:

`L^2-6L`

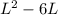
If the area of the rectangle is 135 squared inches, then:

`L^2-6L=135`

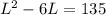
Write the quadratic equation in standard form and use the quadratic formula to find the value of L:

`\begin{gathered} \Rightarrow L^2-6L-135=0 \\ \Rightarrow L=\frac{6\pm\sqrt[]{6^2-4(1)(-135)}}{2} \\ =\frac{6\pm\sqrt[]{36+540}}{2} \\ =\frac{6\pm\sqrt[]{576}}{2} \\ =(6\pm24)/(2) \\ =3\pm12 \end{gathered}`

Then:

`\begin{gathered} L_1=15 \\ L_2=-9 \end{gathered}`

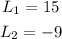
Since L is a length, it cannot be a negative number. Therefore:

`L=15`

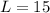
The width of the rectangle is 6 less than the length, so:

`W=9`

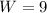
Therefore, the length of the rectangle is 15 inches and the width of the rectangle is 9 inches.