(a)
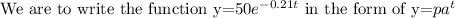
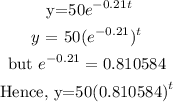
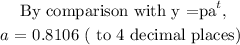
(b)
By comaparing
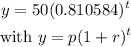
The value of ( 1 + r ) is 0.810584 which is less than 1. This indicates that the exponential function is a decay function.
Thus, ( 1 + r ) = 0.810584
1 + r = 0.810584
r = 0.810584 -1
r = -0.189416
The negative indicates the it is a decay
in percentage, r = 0.189416 x 100
r = 18.9416%
Hence, The annual decay rate is 18.94 % per year
(c)
The continous