Question

4. What is the volume of the cone iſ the area of the base is 147 cm- and the height is 9 cm?

Answer 1

V = 441 cm³ (rounding up to the nearest whole)

1) Since the Volume of the Cone is given by:

`V=(1)/(3)\pi r^2\text{h}`

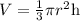
2) The measure of the height is 9cm and the area of the base is 147.

Since the area of a cone is a Circle. Then we can find the radius, applying the Circle Area formula to that:

`\begin{gathered} A_{\text{circle}}=\pi\text{ r²} \\ 147=\pir^2 \\ (147)/(\pi)=(\pi r^2)/(\pi) \\ r^2=46.791 \\ \sqrt[]{r^2}=\sqrt[]{46.791} \\ r=6.84 \end{gathered}`

3) Now that we have that radius we can plug that into the Volume of The cone

`\begin{gathered} V=(1)/(3)\pi r^2\text{h} \\ V=(1)/(3)\pi(6.84)^2\cdot9 \\ V\approx440.94cm^3 \end{gathered}`

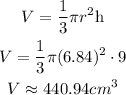
Then the Volume of the cone is approximately 440. 94 cm³ or rounding off to the nearest whole number 441 cm³