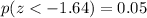Question

Forearm lengths of men, measured from the elbow to the middle fingertip, are normallydistributed with a mean 18.8 inches and a standard deviation 1.1 inches.If 1 man is randomly selected, what is the probability that his forearm length is below 17

Answer 1

Part A

What are the parameters?

The parameters are

We want to find

`p(\mu<17)`

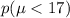
Part B

Find the z score

The formula to use is given by

`z=\frac{\bar{X}-\mu}{\sigma}`
`\begin{gathered} z=\frac{\bar{X}-\mu}{\sigma} \\ z=(17-18.8)/(1.1) \\ z=(-1.8)/(1.1) \\ z=-1.6363636363 \\ z=-1.64 \end{gathered}`

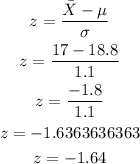
The construction of the standard normal curve is shown below

Part C

We use the standard normal table (from statistical table)

Thus, From statistical table

`p(z<-1.64)=0.05`