Answer
The mass of C4H10 needed = 28 grams
Step-by-step explanation
Given:
The mass of carbon dioxide formed = 85 grams
What to find:
The mass of C4H10 needed to form 85 grams of CO2.
Step-by-step solution:
Step 1: Write the balanced equation for the reaction.
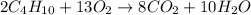
Step 2: Convert 85 grams of CO2 formed into moles.
Using the atomic masses of C and O from the periodic table; the molar mass of CO2 = 44.01 g/mol.
So, the moles of CO2 in 85 grams CO2 can be calculated using the mole formula
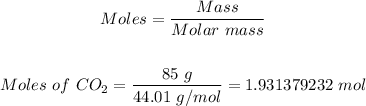
Step 3: Determine the moles of C4H10 needed.
Using the mole ratio of C4H10 to CO2 in step 1 and the moles of CO2 formed in step 2; the moles of C4H10 needed is calculated as shown below.
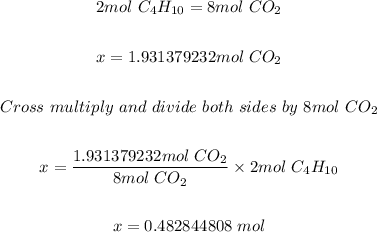
Step 4: Convert the moles of C4H10 in step 3 above to grams.
From the periodic table, the molar mass of C4H10 can be determined to be = 58.12 g/mol.
Using the same mole formula used in step 2, the mass of C4H10 is
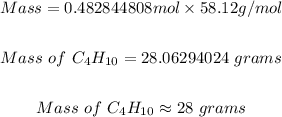
Therefore, the mass of C4H10 needed to form 85 grams of carbon dioxide is 28 grams