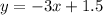Answer:
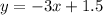
Explanation:
Given the data in the table, to find an equation that represents the same relationship, first, find the slope using any two pairs of points from the table.
Let the two points be:
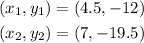
Substitute the points into the slope-formula below:
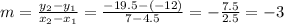
Substitute the slope, m=-3, and the point (4.5,-12) into the slope-intercept form:
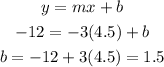
Therefore, the equation of the line in slope-intercept form is: