ANSWER
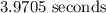
Step-by-step explanation
To find how many seconds it will take to travel 71 feet, substitute the value of d to be 71 feet and solve for t in the equation:
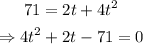
Solve for t using the Quadratic formula:
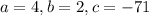
Therefore, we have:
![\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t=\frac{-2\pm\sqrt[]{2^2-(4\cdot4\cdot-71)}}{2\cdot4} \\ t=\frac{-2\pm\sqrt[]{4+1136}}{8}=\frac{-2\pm\sqrt[]{1140}}{8} \\ \Rightarrow t=(-2+33.7639)/(8);t=(-2-33.7639)/(8) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/fxj68hguske0697hn2ddccod6apmeb9wj6.png)
Since time cannot be negative, we only use the first value:
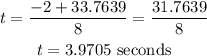
That is the time it will take.