Question

If an arc with a measure of 45 degrees has a length of 32pi inches, what is the circumference of the circle?*

Answer 1

First, we have to find the radius of the circle. Let's use the arc length formula.

`L=2\pi r\cdot(\theta)/(360)`

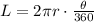
Where L = 32 pi inches, theta = 45. Let's use this information and solve for r.

`\begin{gathered} 32\pi=2\pi r\cdot(45)/(360) \\ r=(32\cdot360)/(2\cdot45) \\ r=(11520)/(90) \\ r=128 \end{gathered}`

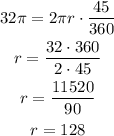
The radius is 128 inches long.

Now, we use the formula for circumference.

`C=2\pi r`

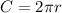
Let's replace the radius we found before.

`C=2\pi\cdot128=256\pi`

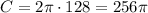
Therefore, the circumference of the circle is 256pi inches.