Answer:
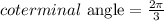
Explanations
The coterminal of angle is determined by adding or subtracting 360 degrees (2pi) from the reference angle.
Given the reference angle in radians as shown:
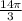
Subtract 360 degerees (2π) from the angle to have
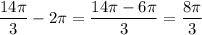
Subtract 2π from the result to have:
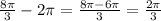
Hence the coterminal angle that lies between 0 and 2π radians is 2π/3 rad