The radius of ferris wheel is r = 29 feet.
The equation for the vertical distance is,
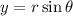
For rotation of 3.5 radians,
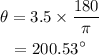
Determine the vertical distance of Josie.
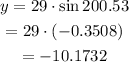
Josie is 10.1732 feet below the horizontal.
Part B:
The distance travelled by Josie is s = 237 feet.
Determine the rotation for distance travelled by Josie.
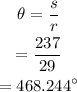
Determine the vertical distance of Josie.
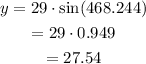
Josie is 27.544 feet above the horizontal.
Part C:
The function for the vertical distance above the horizontal is,
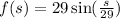
Here angle is in radians.