We have a random sample of size n=64 from a population with mean of 20 and standard deviation of 8.
b) The sampling distribution is the distribution of probabilities for the sample mean.
The expected shape for the sampling distribution is like a normal distribution shape (independently of the population distribution), but this shape will be different depending on the sample size: bigger sample size will have sampling distribution that are less spreaded.
Then, the shape is that of a normal distribution and depends on the sample size.
c) Wehave to calculate the z-score for a sample mean value of 18.7.
We first have to calculate the mean and std. deviation of the sampling distribution:
![\begin{gathered} \mu_s=\mu=20 \\ \sigma_s=\frac{\sigma}{\sqrt[]{n}}=\frac{8}{\sqrt[]{64}}=(8)/(8)=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cxv0fmv2wq9orfo2vnsbjdty2zlyp9plyv.png)
Then, we now can calculate the z-score as:
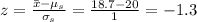
d) We can calculate the z-score in the same way that in the previous point for this new value for the sample mean (sample mean = 20.6):
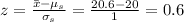
e) We can use the z-score we calculated in point c) and the standard normal distribution to calculate the probability asked:
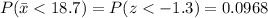
f) We apply the same procedure as point e) to calculate this new probability:
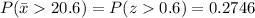
g) We can apply some relations to calculate this probability:
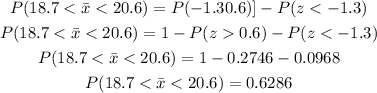
Answer:
b) the shape is that of a normal distribution and depends on the sample size
[Option B].
c) z = -1.3
d) z = 0.6
e) P(xm < 18.7) = 0.0968
f) P(xm > 20.6) = 0.2746
g) P(18.7 < xm < 20.6) = 0.6286