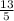The secant of an angle in a right triangle is given by the quotient of the length of the hypotenuse to the length of the side adjacent to it:
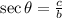
On the coordinate plane, the point (5,12) detmines a right triangle with sides 5 and 12:
Use the Pythagorean Theorem to find the length of the hypotenuse:
![\begin{gathered} H=\sqrt[]{5^2+12^2} \\ =\sqrt[]{25+144} \\ =\sqrt[]{169} \\ =13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sfo20tqqtppobmiqc68gf6ylk1pg4qyun9.png)
Therefore, the exact value of secθ is: