Question

A grocer wants to mix two kinds of nuts. One kind sells for $1.20 per pound, and the other sells for $1.85 per pound. He wants to mix a total of 29 pounds and sell it for $1.65 per pound. How many pounds of each kind should he use in the new mix?

Answer 1

He should use 20.08 pounds of the $1.85 per pound kind of nuts in the new mix

He should use 8.92 pounds of $1.20 per pound kind of nuts in the new mix

Step-by-step explanation:

Let x represent the pounds of $1.20 nut in the mix

Let y represent the pounds of $1.85 nut in the mix

So if he wants to mix a total of 29 pounds, we can set up the below equation;

`x+y=29\ldots\ldots\text{.}\mathrm{}\text{Equation 1}`

If he wants to sell it for $1.65 per pound, we can set up the below equation;

`\begin{gathered} 1.2x+1.85y=1.65*29 \\ 1.2x+1.85y=47.85,\ldots\ldots\text{.}\mathrm{}\text{Equation 2} \end{gathered}`

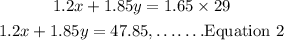
We can now solve the system of equations simultaneously following the below steps;

Step 1: Express x in terms of y in Equation 1;

`x=29-y\ldots\ldots\ldots\text{.Equation 3}`

Step 2: Substitute x with (29 - y) in Equation 2 and solve for y;

`\begin{gathered} 1.2(29-y)+1.85y=47.85 \\ 34.8-1.2y+1.85y=47.85 \\ 34.8+0.65y=47.85 \\ 0.65y=47.85-34.8 \\ 0.65y=13.05 \\ (0.65y)/(0.65)=(13.05)/(0.65) \\ y=20.08\text{ pounds} \end{gathered}`

So he should use 20.08 pounds of the $1.85 per pound kind of nuts in the new mix

Step 3: Substitute y with 20.08 in Equation 3 and solve for x;

`x=29-20.8=8.92\text{ pounds}`

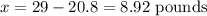
So he should use 8.92 pounds of $1.20 per pound kind of nuts in the new mix