1.
We need to find the roots of the next quadratic function:
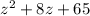
Use the quadratic formula, which is given by the form ax²+bx+c:
![\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/kaoalb540qnvy45obw509ttuwfskx00e99.png)
Replace the values using a=1, b=8 and c=65
![\frac{-8\pm\sqrt[]{(8)^2-4(1)(65)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/w3oy8zhwtfbjtbqg3zlaj9v78pa15nqk5f.png)
![\frac{-8\pm\sqrt[]{64-260}}{2}=\frac{-8\pm\sqrt[]{-196}}{2}=(-8\pm14i)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/br17m0qhwhvc20t95g3cv5qaen8x81ds6w.png)
Simplify the expression:
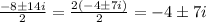
Therefore, the roots of the given expression are:
x = -4+7i
x= -4 - 7i
2.
We need to find the quadratic using the integer coefficients:
We have that the root are :
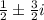
Use the quadratic form ax²+bx+c
The roots are the solution for the quadratic formula, so:
![\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=(1)/(2)\pm(3)/(2)i](https://img.qammunity.org/2023/formulas/mathematics/college/j7f7rkridwprm039m1xxp6awzhfcuwbzqy.png)
Then:
![\frac{1\pm\sqrt[]{9i^2}}{2}=\frac{1\pm\sqrt[]{-9}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/e853ggbmsp8llvd7fb5w2jg7zvr3v42r8o.png)
So we have that 2a =2. then a =2/2
a=1
Also, -b = 1
b = -1
b²-4ac = -9
(-1)²-4(1)c = -9
-4(1)c = -9 -1
-4c = -10
Solve for c
c = -10/-4
c = 5/2
Therefore, with these values, we can replace the quadratic form and we will find the result
a=1
b = -1
c = 5/2
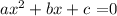
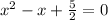
So, the last quadratic is the result.