Answer:
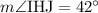 .
.
Explanation:
Start by showing that
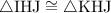 by
by
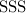 .
.
(Triangle
 and
and
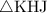 are congruent by side, side, side- all three pairs of corresponding sides are equal in length.)
are congruent by side, side, side- all three pairs of corresponding sides are equal in length.)
From the diagram,
 and
and
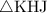 already share two pairs of sides of the same length:
already share two pairs of sides of the same length:
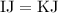 as denoted on the diagram by the short slash.
as denoted on the diagram by the short slash.
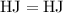 (this side is shared between the two triangles.)
(this side is shared between the two triangles.)
It is also given that
 and
and
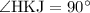 .
.
However,
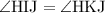 combined with
combined with
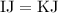 and
and
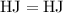 would not be sufficient for showing that
would not be sufficient for showing that
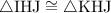 by side, angle, side (
by side, angle, side (
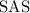 .) Two triangles are congruent by
.) Two triangles are congruent by
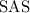 only if angle that is equal is between the two pairs of sides.
only if angle that is equal is between the two pairs of sides.
Since
 and
and
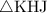 are both right triangles, the Pythagorean Theorem would apply:
are both right triangles, the Pythagorean Theorem would apply:
 in
in
 .
.
Likewise:
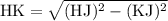 in
in
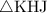 .
.
Since
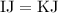 :
:
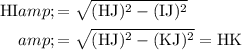 .
.
Therefore,
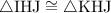 by
by
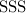 (
(
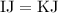 ,
,
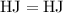 , and
, and
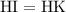 .)
.)
By congruency,
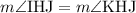 .
.
Thus,
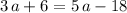 . Solve this equation to get
. Solve this equation to get
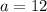 .
.
Therefore,
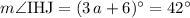 .
.