ANSWER
12, 36, 108 and 324.
EXPLANATION
We want to find 4 geometric means between 4 and 972.
Let w, x, y and z be the four geometric means.
So, we have that:
4, w, x, y, z, 972
The first term, a, of this progression is 4.
The 6th term is 972
We have that the nth term of a geometric progression is:
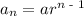
Let us find r by using the 6th term:
![\begin{gathered} 972\text{ = 4 }\cdot r^{6\text{ - 1}}\text{ = 4 }\cdot r^5 \\ r^5\text{ = }(972)/(4)\text{ = 243} \\ r\text{ = }\sqrt[5]{243} \\ r\text{ = }3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6tj2vwo6at78qiwiyomu4bswqzrhdw6ba6.png)
Now, let us find the four terms:
=> w is the second term, so n = 2:

=> x is the thrid term, so n = 3:
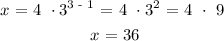
=> y is the fourth term, so, n = 4:
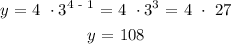
=> z is the fifth term, so n =5:
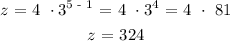
So, the four geometric means are 12, 36, 108 and 324.