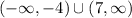
Step-by-step explanation
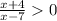
Step 1
Multiply both sides by (x-7)
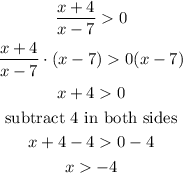
Check possible critical points.
x=-4
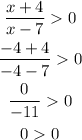
so, test each interval for a positive or negative result, the divide ths igns
we need a result greater than zero ( so a positive number)
therefore, the answer is
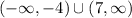
I hope this helps you