Solution:
Given:

Number of ways to order chicken
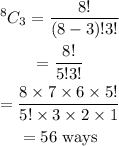
Number of ways to order steak
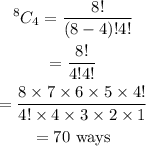
Number of ways to order lobster
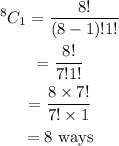
Hence, the number of ways one can order 3 chicken, 4 steaks, and 1 lobster is;
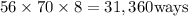
Therefore, the number of ways one can order 3 chicken, 4 steaks and 1 lobster is 31,360 ways