Answer:
(a)Two real solutions.
(b)No real solution
Step-by-step explanation:
The discriminant of a standard quadratic function y=ax²+bx+c is obtained by using the formula:
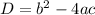
Part A
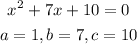
Therefore:
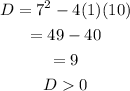
Since D is greater than 0, the quadratic equation has two distinct real solutions.
Part B
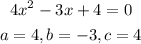
Therefore:
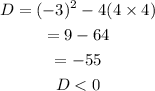
Since D is less than 0, the quadratic equation has No real solution.