Question

What are the Equilibrium concentrations of each gas after the equilibrium is established ? (ICE Chart is required)

Answer 1

1st) It is necessary to calculate the concentration in molarity of the gases that are initially in the vessel:

`\begin{gathered} 2L-0.15\text{moles} \\ 1L-x=\frac{1L\cdot0.15\text{moles}}{2L}_{} \\ x=0.075\text{moles} \end{gathered}`

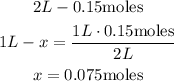
So, initially the concentration of the gases (bromibe and chlorine) is 0.075 M.

2nd) We can write what happens during the initial stage, change and equilibrium:

Reaction: Br2(g) + Cl2(g) ----> 2 BrCl(g)

Initial: 0.075M 0.075M 0.0375

Change: -x -x 2x

Equilibrium: 0.075M-x 0.075M-x 0.0375+2x

3rd) Now with the Kc value we can replace the equilibrium data and solve:

`\begin{gathered} K_c=(\lbrack BrCl\rbrack^2)/(\lbrack Br_2\rbrack\cdot\lbrack Cl_2\rbrack) \\ K_c=\frac{(0.0375+2x)^2}{(0.075-x)\text{.(0.075-x)}} \\ 7.0=(0.0014+0.15x+4x^2)/(0.0056-0.075x-0.075x+x^2) \\ 3x^2-1.2x+0.0392=0 \end{gathered}`

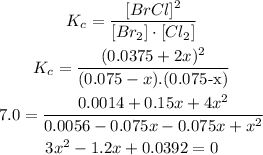
So far we get 2 values of x, 0.036 and 0.36. We can only use one of them, to find out wich one we have to use, it is important to see the value in the equilibrium.

Since the highest concentration from which we subtract the value of x is 0.075M, we must choose 0.036 instead of 0.36, otherwise we would not be able to subtract them.

4th) Finally, we replace the value of x in the concentrations of the equilibrium. So, the equilibrium concentrations are:

[Br2]= 0.039 M

[Cl2]= 0.039 M

[BrCl]= 0.1095 M