Given the following interior angle of a regular polygon:

You need to remember that, by definition, a regular polygon is a polygon whose sides have all equal lengths.
Therefore, you can apply the following formula:
Where "n" is the number of sides of the polygon and β is the measure of one interior angle of the polygon.
Knowing that, in this case:
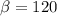
Therefore, you can substitute this value into the formula and solve for "n":
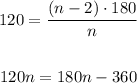
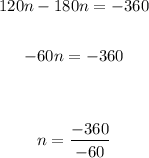

Hence, the answer is:
