Question

A red die is tossed and then a green dieis tossed. What is the probability thatthe red die shows an even number orthe green die shows an even number?Make sure your answer is reduced.3[?]Hint: The two events are not mutually exclusive. Soto the find the probability of the union, use:P(A or B) = P(A) + P(B) - P(A and B)L

Answer 1

Given:

A red die is tossed and then a green die is tossed.

Required:

We have to find the probability that the red die shows an even number or the green die shows an even number.

Step-by-step explanation:

Let A denotes the event that the red die shows an even number and B denote the event that the green die shows an even number.

Here the total number of outcomes is 6(1-6) and the number of favorable outcomes are 3(2, 4, 6).

Then we have

`\begin{gathered} P(A)=(3)/(6)=(1)/(2) \\ \\ P(B)=(3)/(6)=(1)/(2) \end{gathered}`

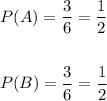
Therefore,

`P(A\text{ and }B)=(1)/(2)*(1)/(2)=(1)/(4)`

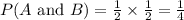
Hence the probability that the red die shows an even number or the green die shows an even number is

`\begin{gathered} P(A\text{ or }B)=P(A)+P(B)+PA(A\text{ and }B) \\ \\ =(1)/(2)+(1)/(2)-(1)/(4) \end{gathered}`
`\begin{gathered} =1-(1)/(4) \\ =(3)/(4) \end{gathered}`

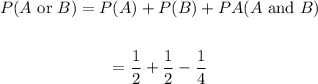
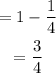
Final answer: