From the table, we can deduce the following:
(x, y) ==> (45, 56), (42, 52), (43, 51), (41, 48), (49, 58), (46, 45), (43, 45), (41, 50), (35, 46)
Let's find the correlation coefficient.
To find the correlation coefficient, apply the formula:
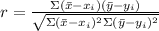
Where:
xi is the mean of the x-variables
yi is the mean of the y-variables.
Thus, we have:

Now, for the correlation coefficient, we have:
![\begin{gathered} \Sigma(x-x_i)^2=(45-42.8)^2+(42-42.8)^2+(43-42.8)^2+(41-42.8)^2+(49-42.8)^2+(46-42.8)^2+(43-42.8)^2+(41-42.8)^2+(35-42.8)^2 \\ \Sigma(x-x_i)^2=121.6 \\ \\ \Sigma(y-y_i)^2=(56-50.1)^2+(52-50.1)^2+(51-50.1)^2+(48-50.1)^2+(58-50.1)^2+(45-50.1)^2+(45-50.1)^2+(46-50.1)^2 \\ \Sigma(y-y_i)^2=174.9 \end{gathered}]()
Solving further:
![\begin{gathered} \Sigma(x-x_i)(y-y_1)=(45-42.8)(56-50.1)+(42-42.8)(52-50.1)+(43-42.8)(51-50.1)+(41-42.8)(48-50.1)+(49-42.8)(58-50.1)+(46-42.8)(45-50.1)+(43-42.8)(45-50.1)+(41-42.8)(50-50.1)+(35-42.8)(46-50.1) \\ \\ \Sigma(x-x_i)(y-y_i)=79.2 \end{gathered}]()
Now, plug in the values in the formula and solve for r.
We have:
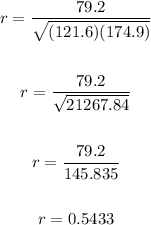
Therefore, the correlation coefficient is 0.5433
• ANSWER:
0.5433