From the law of cosines, for a given triangle with sides a, b, and c with corresponding opposed angles A, B, and C, the following condition is satisfied:

Isolate the cosine of the angle C from the formula:
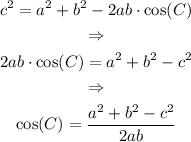
Use the inverse cosine function to isolate the angle C:
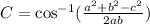
Evaluate the expression using a calculator by substituting a=19, b=16 and c=11:
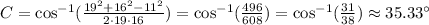
The other angles can be obtained using the law of cosines applied to the other angles:
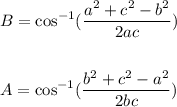
Another way is to use the law of sines.
Since the side c and the angle C are now known, we can write down:
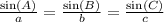
Use the equation that relates the angles A and C to isolate A:
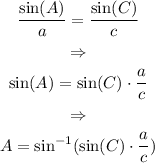
Substitute C=35.33°, a=19 and c=11:
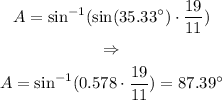
To get the angle B, we can use the method of the law of sines:
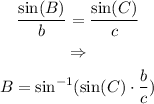
Or we can use the fact that for any triange, the sum of its internal angles must be 180°:
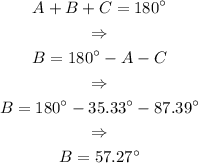
Notice that some decimal figures may vary, as we are not writing all the digits to use our calculations.
Notice that for the first angle the only option was to use the law of cosines.
For the second angle we were able to use wheter the law of cosines or the law of sines.
For the last angle we were able to use those two formulas, or we could find it via a third way using the sum of the internal angles of a triangle.
Nevertheless, the law of cosines is the most straightforward method to find those angles because it does not involve knowing the other two. Additionally, this would allow the results to be as precise as possible because we are not ignoring any decimals to use the formula.
Therefore, the angles are:
A=87.39°
B=57.27°
C=35.33°