We are given that the measure of the following angles is the same:
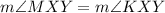
And, by the vertical angles theorem we know that:
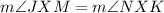
Now, the "Angle Addition Postulate" states that the measure of an angle is equal to the sum of the measure of smaller angles in between.
Applying the postulate to angle MXY we get:
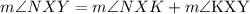
And, applying the postulate to angle JXY we get:
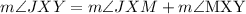
Now, we subtract the equations, we get:
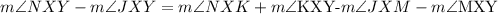
From the initial statement, we can cancel out the measure of angles KXY and MXY since they are equal:
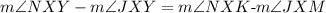
Also, from the vertical angles theorem we can cancel out the measure of angles NXK and JXM:
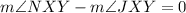
Now, we add the measure of angle JXY:
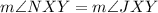
Therefore, the conclusion is option D.