Question

Question 8If it takes the same amount of time for a planet to move from point A to point B as itdoes for a planet to move from point C to point D, then what must a planet do interms of its speed in each sector?Sector 2Sector 116

Answer 1

We are given that to a planet takes the same amount of time to go through two different sectors. The speed of the planet (distance over time) when goes through sector AB is:

`v_(AB)=(S_(AB))/(t)`

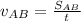
Where

`\begin{gathered} S_(AB)=\text{distanve from A to B} \\ t=\text{time} \end{gathered}`

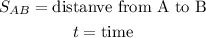
And the speed from C to D is:

`v_(CD)=(S_(CD))/(t)`

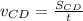
Where:

`\begin{gathered} S_(CD)=\text{distance from C to D} \\ t=\text{time} \end{gathered}`

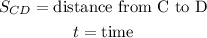
We can solve for the time in each equation and we get:

`\begin{gathered} t=(S_(AB))/(v_(AB))_{} \\ \\ t=(S_(CD))/(v_(CD)) \end{gathered}`

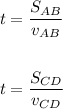
Since time is the same we can equate both equations:

`(S_(AB))/(v_(AB))=(S_(CD))/(v_(CD))_{}_{}`

Now we can cross multiply:

`v_(CD)S_(AB)=v_(AB)S_(CD)`

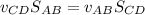
Solving for the speed CD:

`v_(CD)=(v_(AB)S_(CD))/(S_(AB))`

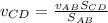
Since the distance CD is larger than the distance AB this means that:

`(S_(CD))/(S_(AB))>1`

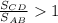
Since the ratio is larger than 1, this means that speed CD is larger than speed AB:

`v_(CD)>v_(AB)`

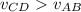
This means that the planet will speed up at CD and slow down at AB.