The slope-intercept form of a line is:
y = mx + b
where m is the slope and b is the y-intercept
The slope of the line that passes through the points (x1, y1) and (x2, y2) is computed as follows:

Restaurant warehouse's line passes through (5, 262.2) and (10, 427.15). Its slope is:

Supply side's line passes through (5, 202.2) and (10, 382.15). Its slope is:
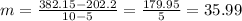
Replacing with the point (5, 262.2) and m = 32.99 in the general equation:
262.2 = 32.99(5) + b
262.2 - 164.95 = b
97.25 = b
Replacing with the point (5, 202.2) and m = 35.99 in the general equation:
202.2 = 35.99(5) + b
202.2 - 179.95 = b
22.25 = b
Then, the equations are:
r(n) = 32.99n + 97.25
s(n) = 35.99n + 22.25
If both restaurants charge the same, then r(n) = s(n)
32.99n + 97.25 = 35.99n + 22.25
97.25 - 22.25 = 35.99n - 32.99n
75 = 3n
75/3 = n
25 = n
r(25) = 32.99(25) + 97.25 = 922
Both restaurants charge $922 for 25 cases of paper towels