Question

A reverse bungee jump can be modeled by the function f(x)= -60x^2 + 120x. Find the maximum height.​

Answer 1

x = 1, y = 60 or (1, 60)

Explanation:

Given the quadratic function, f(x) = -60x² + 120x, which models a reverse bungee jump. If we graph this given quadratic function, then it will show a downward-facing parabola whose vertex is the maximum point on the graph.

Solution:

We can determine the maximum height of the given quadratic function by using the formula to find the x-coordinate of the vertex:

`\displaystyle\mathsf{x\:=(-b)/(2a)}`

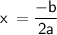
From the given quadratic function: f(x) = -60x² + 120x, where a = -60, b = 120, and c = 0:

Substitute the given values for a and b into the formula for finding the x-coordinate value of the vertex:

`\displaystyle\mathsf{x\:=(-b)/(2a)\:=\:(-120)/(2(-60))\:=(-120)/(-120)\:=1}`

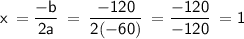
Now that we have the value for the x-coordinate of the vertex, x = 1, substitute this value into the given quadratic function to find its corresponding y-coordinate:

f(x) = -60x² + 120x

f( 1 ) = -60( 1 )² + 120( 1 )

f( 1 ) = -60 + 120

f( 1 ) = 60

Thus, the y-coordinate of the vertex is f(x) = 60.

Final Answer:

Therefore, the maximum height of the reverse bungee jump is x = 1, y = 60 or (1, 60).