Question

the sides of a larger square are 16 cm. The midpoints of the sides are joined to form a new square. Find the sum of areas of all squares

Answer 1

To understand this question we have to draw a figure that shows the information given

The area of the largest square is

`A=S^2=(16)^2=256`

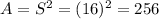
Since the diagonal of the smaller square is equal to the side of the larger square, then we will find its area using the rule of the diagonal

`A_s=(d^2)/(2)=((16)^2)/(2)=128`

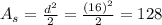
Then the common ratio between the two squares is 1/2

So they can form a geometric sequence with a common ratio of 1/2 and first term 256

Since there are 7 squares, then

n = 7

Let us find the sum of their areas

The rule of the sum of the geometric sequence is

`S_n=(a(1-r^n))/(1-r)`

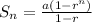
Where:

a is the first term

r is the common ratio

n is the number of terms

a = 256

r = 1/2

n = 7

Substitute them in the rule

`\begin{gathered} S_7=(256(1-\lbrack(1)/(2)\rbrack^7))/(1-(1)/(2)) \\ S_7=508 \end{gathered}`

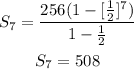
The sum of the areas of the squares is 508 cm^2