25. As we see that the y-coordinates does not change, it must be a reflection on a vertical axis. This is a axis of reflection x= constant.
We can use the x-coordinates of the preimage and the image of one point to calculate the axis of reflection, as it has to be in the midpoint:
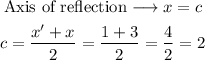
The axis of reflection is x=2.
26. In this case, we have an horizontal axis of reflection y=c.
We can find c by calculating the midpoint between the y-coordinates of a point before and after the transformation.
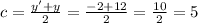
The axis of reflection is y=5.
27. Axis of reflection y=-5
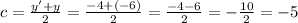
28. This is a line that acts as axis of reflection.
This line is y=-x.
Then we can write the transformation as:
