Given:
Angle of inclination = 5 degrees
Distance = 4,955 feet
Let's find the driver's altitude.
Let's first sketch a figure which represents this situation.
To find the altitude, apply the trigonometric ratio for sin:
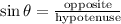
Where:
The opposite side is the altitude
The hypotenuse = 4955 ft.
θ = 5 degrees
Thus, we have:
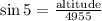
Multiply both sides by 4955:

Therefore, the dirver's increase in altitude is 432 ft.
ANSWER:
432 feet