Question

cos eand sin 0 < 0. Identify the quadrant of the terminal side of e andfind sin eO A. Quadrant: IVsin35O B. Quadrant: IVsin 0 -34C. Quadrant: 111sin3D. Quadrant: 11sin 0 = 1

Answer 1

Given

`\begin{gathered} \text{Cos}\theta=(4)/(5) \\ sin\theta<0 \end{gathered}`

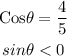
Required

To find the quadrant of terminal side of θ and sinθ

Step 1

Find the opposite

Using the trig ratio CAH(cosine, adjacent, hypothenuse)

`\begin{gathered} \cos \theta=\frac{adjacent}{\text{hypothenuse}} \\ so\text{ that from the question} \\ \text{adjacent = 4 } \\ \text{and the} \\ \text{hypothenuse = 5} \end{gathered}`

We can find the opposite using pythagoras theorem, which is expressed as

`\begin{gathered} \text{hypothenuse}^2=opposite^2+adjacent^2 \\ 5^2=opposite^2+4^2 \\ \text{opposite}=\sqrt[]{25-16} \\ \text{opposite = }\sqrt[]{9} \\ \text{opposite = 3} \end{gathered}`

Step 2

Find sinθ

Using the trig ratio SOH (sine, opposite ,hypothenuse), we can find sinθ as follows

`\begin{gathered} \sin \theta=\frac{opposite}{\text{hypothenuse}} \\ \sin \theta=(3)/(5) \end{gathered}`

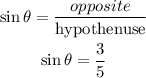
Final Step

Find the quadrant of the terminal side of θ and sinθ

Since sinθ <0, this means that sinθ is negative

Therefore the right answer is

sinθ = 3/5 and it is in quadrant IV because that is where cosine is positive..

Final answer: option A