Step-by-step explanation
In this question, we have the following information;
r = 0.022% annual rate
k = 12since we’re withdrawing monthly
N = 1515 years
P = $400,000 we are beginning with $400,000
d= regular withdrawal
We would be using the formula for Payout annuity below;
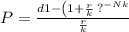
Therefore, we have that;
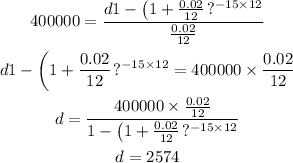
Answer:$2574