the Given,
The mass of the 1st train car, M=15000 kg
The mass of the 2nd train car, m=14000 kg
The initial velocity of the 1st train car, u₁=4.0 m/s
The initial velocity of the 2nd train car, u₂=0.7 m/s
The time it takes for the trains to come to a stop, t=3 s
From the law of conservation of momentum, the total momentum of a system always remains constant.
Thus,
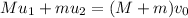
Where v₀ is the velocity of the coupled trains after the collision.
On substituting the known values,
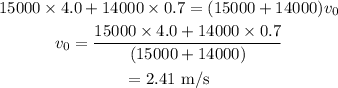
Thus the final velocity of the trains is 2.41 m/s
Given that the trains come to a stop after 3 seconds of the collision.
That is the final velocity of the trains after the 3 seconds of collision is v=0 m/s
From the equation of motion,
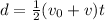
Where d is the distance for which the trains slide before coming to a stop.
On substituting the known values,
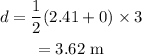
Thus the trains slide for 3.62 m after collision before coming to a stop.