Question

When will the population reach half of its original value?

Answer 1

Let the oak tree population be represented as y.

The rate of population decrease = 8% per year

Since the population continues to decrease at a constant rate, the population size of the oak tree at the end of each year is evaluated as

`\begin{gathered} P(t)=P_0(1-r)^t\text{ ------ equation 1} \\ \text{where} \\ P_0\Rightarrow the\text{ inital poplulation size of the oak trees} \\ t\Rightarrow period,\text{ in years} \\ r\Rightarrow\text{ rate of population decrease} \\ \\ \end{gathered}`

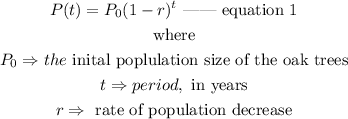
Thus, when the population reaches half its original value,

`\begin{gathered} P(t)_{}=(y)/(2)\text{ (half the or}iginal\text{ value)} \\ P_0=y\text{ (original value)} \\ r\text{ = 0.08 } \\ t\text{ is the period, which is unknown.} \end{gathered}`

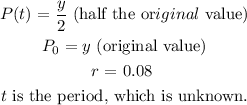
Substitute the above values in equation 1

`\begin{gathered} (y)/(2)=y(1-0.08)^t \\ (y)/(2)=y*0.92^t \\ \Rightarrow(1)/(2)=0.92^t \\ \end{gathered}`

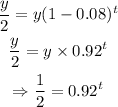
Take the logarithm of both sides

`\begin{gathered} \log _{}((1)/(2))=log(0.92^t) \\ \Rightarrow\log _{}((1)/(2))=t* log(0.92^{}) \\ -0.30=t*-0.036 \\ -0.30=-0.036t \end{gathered}`

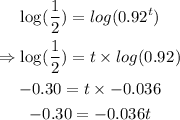
Divide both sides by the coefficient of t

`\begin{gathered} \text{the co}efficient\text{ of t is -0.036.} \\ \text{thus,} \\ (-0.30)/(-0.036)=(-0.036t)/(-0.036) \\ \Rightarrow t=8.33 \end{gathered}`

Hence, the population will reach half of its original value in approximately 8.3 years (nearest tenth).