Question

1. Which point is NOT on the graph represented by y = x^2 + 3x - 6? A. (-6, 12) B. (-4,-2) C. (2,4) D. (3,-6)2. What is an equation of the line that passes through (-2,3) and (6,-1)?

Answer 1

If a point is in the graph of the parabola it needs to satisfy the equation. So we just need to find which values does not satisfy the equation

`(-6)^2+3(-6)-6=12,`

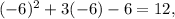
then the number A. IS on the graph

`(-4)^2+3(-4)-6=-2,`

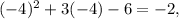
then the number B. IS on the graph

`(2)^2+3(2)-6=4,`

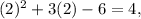
then the number B. IS on the graph, and finally

`(3)^2+3(3)-6=12,`

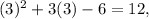
since this is diferent from -6, then (3,-6) is NOT on the graph. Then the answer is D. (3,-6)

The point-slope form is

`y-a=m(x-a)`

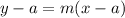
we find the slope using the formula

`m=(-1-3)/(6-(-2))=(-4)/(8)=-(1)/(2)`

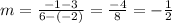
Replacing this, and the point (-2,3)

`\begin{gathered} y-(-2)=-(1)/(2)(x-3) \\ y+2=-(1)/(2)x+(3)/(2) \\ 2y+2=-x+3 \\ x+2y=1 \end{gathered}`

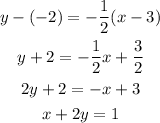
The equation of the line is x+2y=1